We are now on the verge of a second quantum revolution driven by quantum information science. Quantum coherence and correlations define the distinguishing features of second-generation quantum technologies, differentiating them from their predecessors. We explore how the concepts of quantum coherence and correlations can be updated in situations where measurement statistics cannot be encoded using conventional methods. In standard quantum mechanics, the state vector of a pre-selected system provides a probability distribution for the statistics of ideal measurements. It directly enters into the calculation of average values of physical observables. When the information on the pre-selected system is somehow less than the maximum, state vector formalism becomes insufficient. Consequently, we move on to density matrix formalism to encode all measurement statistics by a single mathematical object. In this case, the density matrix, a statistical mixture of state vectors, has the minimum number of parameters to calculate the averages of observables. Algebraically, a density matrix is a Hermitian, positive-semidefinite, and normalized operator that acts on the Hilbert space. However, both state vector and density matrix formalisms are sometimes inadequate due to computational or conceptual difficulties. Our research agenda in quantum information aims to overcome such obstacles by identifying and characterizing alternative mathematical objects that can encode the measurement statistics of the physical systems whose states cannot be represented efficiently in standard quantum mechanics.
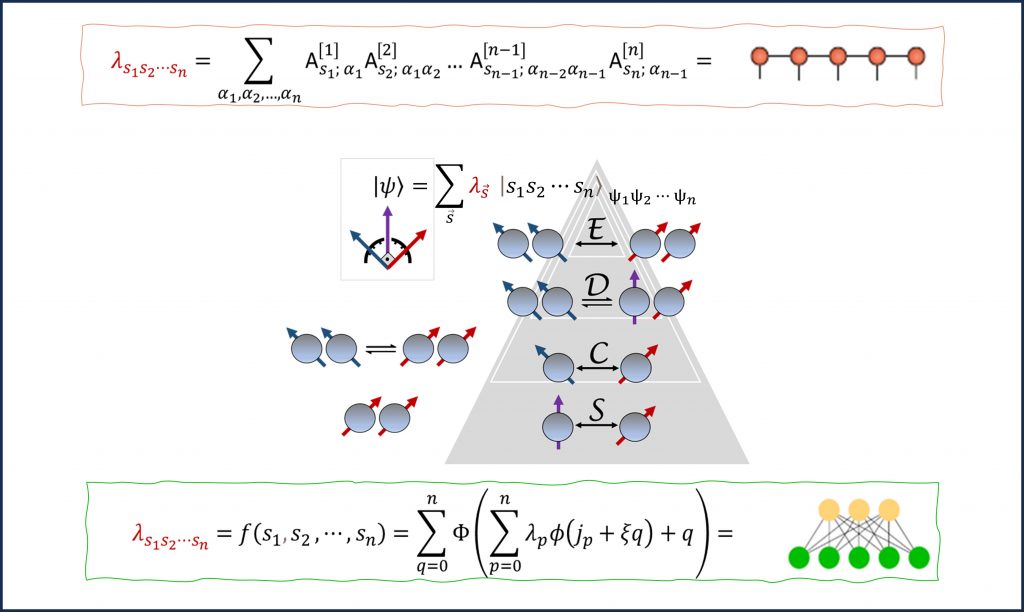
The strongly correlated many-body quantum states are essential in quantum chemistry and condensed matter physics. However, achieving an accurate theoretical characterization can be computationally complex, leading to a trade-off between the accuracy and cost of the computation.
In many cases, the state of interest corresponds to a superposition of well-defined basis states. However, when the superposition contains numerous terms, it becomes challenging to compute the optimal set of probability amplitudes that characterize the state vector. One solution is the representation of probability amplitudes as a network, such as a rank-n tensor or a multilayer neural network, to reduce computational complexity. We aim to utilize these representations to examine the nature of multipartite quantum correlations.
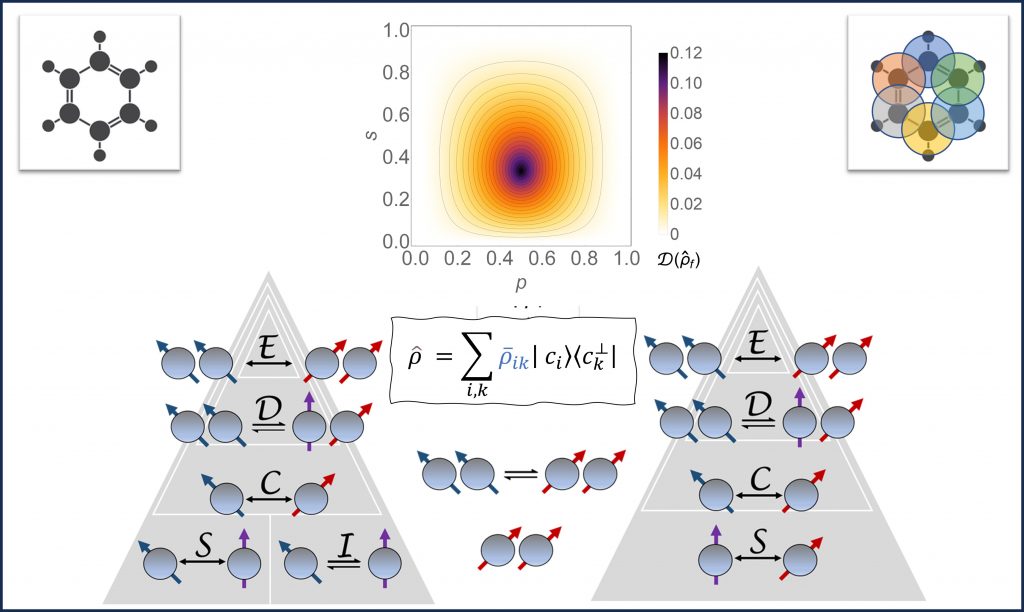
The resource theory of quantum superposition aims to quantify and manipulate the nonclassicality in the superposition of nonorthogonal states. Previous studies have overlooked the overlaps associated with the indistinguishability of these states. However, these overlaps can also give rise to quantum correlations, and omitting them can create conceptual inconsistencies. To resolve these inconsistencies, we presented a unified framework for inter-basis quantum superposition and quantum state indistinguishability in a recent paper [U.2]. To achieve this, we utilized the notion of biorthogonality and represented the nonorthogonal systems by a non-Hermitian but trace-one state whose eigenvalues are real.
We plan to extend this study to explore the role of quantum superposition in the hierarchy of nonclassicality. We believe the biorthogonal framework can lead us to a complete theory of nonclassicality that unifies contextuality, superposition, coherence, and discord.
Furthermore, a chemical bond between two atoms is closely associated with overlapping nonorthogonal atomic orbitals. Therefore, biorthogonal information theory can deepen our understanding of the nonclassicality in the phenomena of chemical bonding [U.6]. For example, chemists have been searching for a comprehensive and conventional definition of aromaticity for almost two centuries. However, we continue to discover new types.
Exploring the correlations shared between systems occupying overlapping regions in space is not only crucial for understanding chemical phenomena. It also holds great significance for designing devices such as quantum computers consisting of indistinguishable particles like electrons. Through the biorthogonality framework, we intend to delve deeper into this area of research.
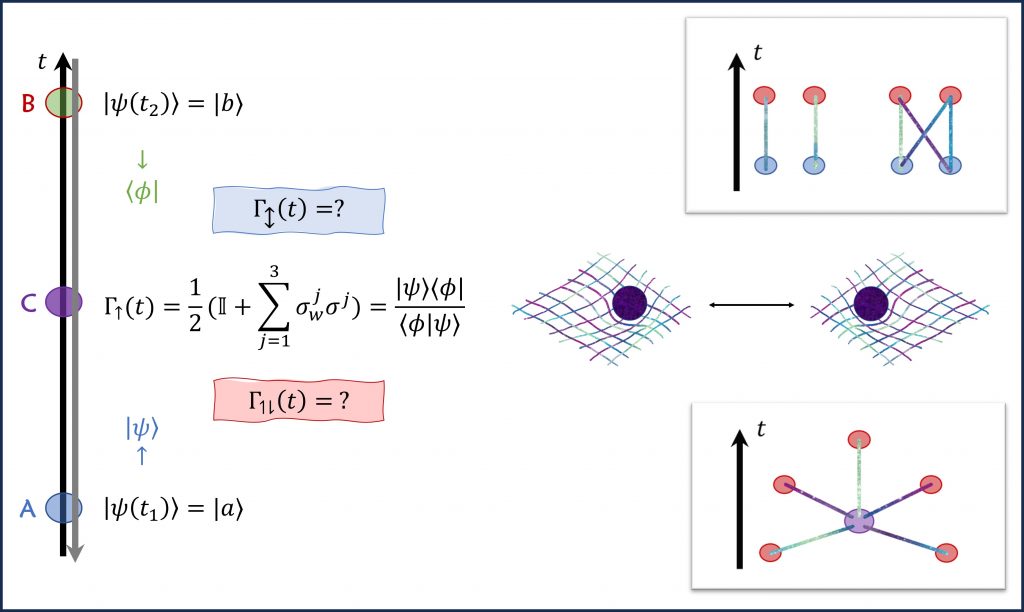
We are deeply interested in exploring temporal quantum correlations using pseudo-density matrix/operator (PDO) representation. The PDO is a powerful tool for extending density operators to include temporal correlations between systems measured at different times. The idea is to combine time-like separated subsystems with the tensor products, like space-like separated subsystems. When a PDO breaks down the positivity condition and yields a negative eigenvalue, this indicates the presence of correlations in time, as first pointed out by R. Feynman in 1987.
In a recent paper with our collaborators [U.1], we investigated the relationship between PDOs and different spacetime formalisms of nonrelativistic quantum mechanics, such as the two-state (or time-symmetric) vector formalism and indefinite causal structures. Previous studies of (in)definite causal orders have relied on quantum supermaps rather than quantum states, such as quantum combs, process matrices, and quantum SWITCHs. In our paper, we introduced the notion of a single-time PDO to encompass previous works and approaches. We found that weak measurements are sufficient to investigate the relation between the state at a given time and the uncertainty in the order of events before and after it. We also proposed experimental realizations of witnessing superpositions of causal orders by weak measurements.
Our research direction is crucial for generalizing the notion of quantum states to quantum gravity scenarios where spacetime is quantized. It has also potential implications on quantum technologies. For instance, one of our primary objectives is to embark on the design of indefinite casual order algorithms and protocols that hold immense potential in the realms of quantum communication and quantum cryptography technologies.